In last post, we observed that the price of options is always changing. Risk is a slippery matter, and option premiums are always reflecting the changing prices of stocks and amount of perceived risk in the market. There are three elements that go into the price, and now I'll will show you how to calculate that price. Known as the Greeks: Delta, Theta, Beta and Vega are the ones used in the HOT Trading System. Don't worry, there's no difficult math involved. You just need to know how to find the important information on your thinkorswim platform.
Scenario One: You think AAPL is going to to go up. You decide to use Call options. But which one should you buy? How much will you make if the price goes up?
Lets take a look at the option chain.
On the left you see Call option chain and on the right the Put option chain, with the strikes down the middle. The ones in gold color are "in the money" and those in the white area are "out of the money". On the left of each kind you will see a column called "Delta". Put deltas are always written as a negative number, and Call deltas as a positive number. ITM options always have a delta between 1.00 and 5.00 and OTM options always have a delta of less than .5. For example, an April 160 option with a delta of -.35 must always be an OTM Put.
With the Christmas retail season coming up, you predict that the price of the stock will rise, so you decide to buy AAPL December Calls. You see that AAPl is currently priced at 97.67 and if you look on the left most column, you see "Delta" and can find the December 80 Call with a delta of 100. The asking price for the ATM Call (97.5) is $4.20 and the delta is .53. That means that each contract (100 shares) will cost you $420.00 to trade, and when the stock goes up, the option will begin to move at 53 cents (the delta) for every dollar the price of AAPL goes up, However, if you think the price will go over $100 by December, then you could buy the December 100 strike and control 100 shares for $3.05, with a delta of .43. The higher the price of the Call strike, the lower the delta. But what if you wanted the value of your Call option to match that of the stock price? You would need a delta close to 1.00. That means buying the December 80 Call with a delta of 1.00, for the price of $18.10 per share.
Why would anyone want to do that? If you bought 100 shares of AAPL and hoped they would go up, you'd need over $9,767. But if you simply buy the December 80 Call, you could get the same benefit for only $1,810 per 100 shares. Similarly, if you think the price of AAPL will go down, and you want to take advantage of that move, you could buy a Deep-ITM December Put at a strike of 120 and delta of -.90, meaning that your Put will increase by 90 cents for every dollar the price goes down. Less capital means less risk. That's one of the benefits of knowing your delta!
Delta is the rate of change between the price of a stock and a price of an option. It includes the total price, including both intrinsic and extrinsic elements such a time value. To get an option that mimics the action of the actual stock, you need a deep-ITM Call or Put. In our trading, that means only buying options with a delta of .70 or greater.
So now you know what delta is, how to find it, and how to use it.
Last week we talked about the time decay of options. Time means money, and sellers of options have to calculate the length of the option when pricing it. If you take the total value of an option and divide it by the number of days until expiration, you end up with a number we call THETA. If you bought an OTM option worth $2.10 and it expires in ten days, then your theta is -.21 X 100 shares or -$21 per day. If you sold an OTM option for $4.00 and it expires in 16 days, then your theta is 2.5 X 100 or $250 per day. Of course, these are averages, and the actual amount each day may vary.
ITM options have quite low theta as most of the price is intrinsic value. OTM have all theta. ATM options have a mix of the two. This is true whether we are talking Puts or Calls.
In the HOT Trading System, theta is the primarily tool of wealth creation. Although both intrinsic and extrinsic values of an option are important, it is theta which is certain to decay, creating profits for us, while delta may go up and down over time and as prices change.
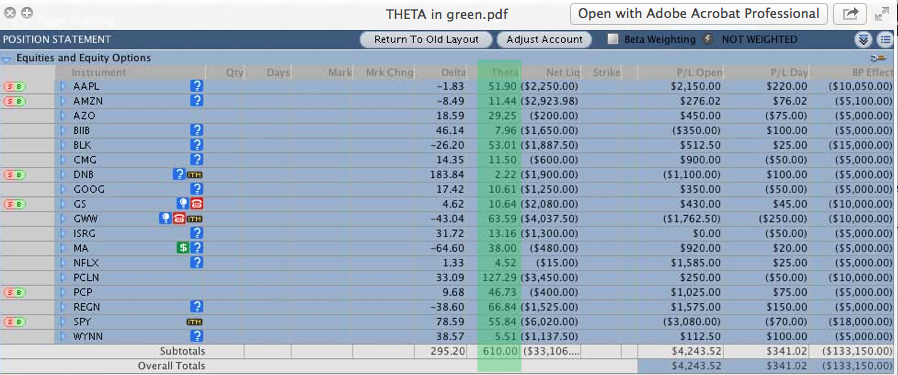
In this screenshot of an account, you will see the theta marked in green.
You see the amounts of theta for each position, and the total which is 610. This means that at current prices, the account is growing at $610 per day.
The volatility element in the price of an option can be measured by comparing the price action of the stock with the general market. In the USA, the SPY index is considered a standard and is given a Beta value of 1.00, while all other stocks can be compared to it. This much almost everyone knows, but in fact the real story is what the numbers mean.
If the Beta is it means
1.0 same volatility as market
>1.0 more volatile than market
<1.0 less volatile than market
0 volatility unrelated to market
-1.0 volatility is contrary to market
To find the beta of any stock on thinkorswim, simply type in the symbol and click to open up basic information. You'll find the beta listed on the right side.
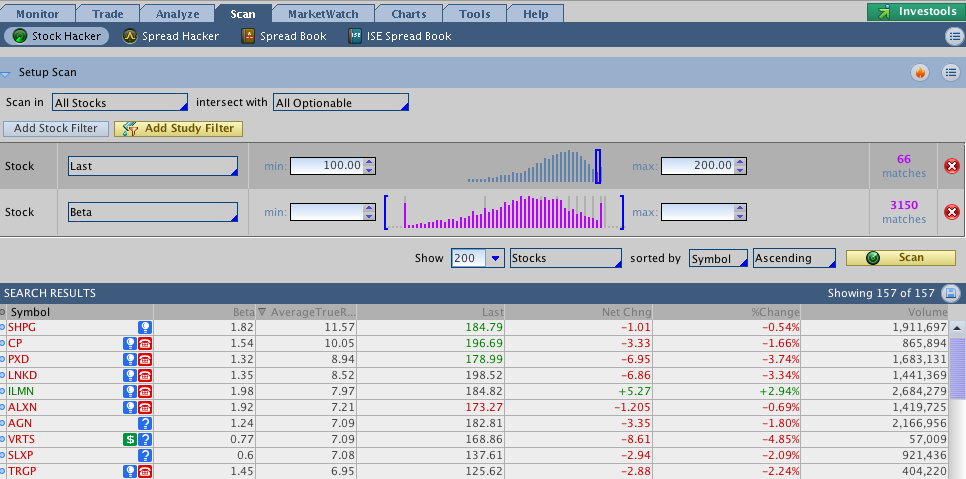
To search for stocks within any range for beta, set up and select the Scan tab as follows:
You will see I've scanned for stocks between 100 and 200, and then sorted by Beta-ness. I also added a column for ATR (Average True Range) as well so we can compare to the Beta value. You can adjust the parameters on the Price Range and Beta functions to narrow down or wider your search. For example, if you are looking for stocks with higher beta ( >1.3 ) then you will find lots of them right here.
Because the HOT Trading System prefers higher premiums when we sell puts and calls, then the Beta function can help us find stocks that generate more premium.
There's a lot more to learn about Beta, so if you want to jump in the deep end, start here.
The second aspect of volatility is how options on a stock compare to themselves over time. Sometimes a stock might have a dramatic announcement, creating uncertainty or anxiety among investors. At that moment, the price of the stock may or may not move, but uncertainty may pump up option premiums. Another case is where there are takeover rumors, or an impending earnings announcement, or pending FDA approval on a drug. That measured by Vega.
Vega is the way we measure the changing effect of the implied volatility in a stock, and according to Investopedia, is " the amount that an option contract's price changes in reaction to a 1% change in the volatility of the underlying asset." Vega is also related to time, as the closer an option is to expiration, the less Vega it would have. In this example, we see that volatility values for IBM ATM Puts and Calls would be inflated by approximately .31 (in blue) if IBM became more volatile.
Vega is important to understand because traders who use credit spreads can find their spreads widening instead of narrowing, even if the stock price doesn't change. This can occur whenever the general market become more volatile, or an individual stock has a volatility event, such as an impending earnings announcement. If you sell an Iron Condor, then both Puts and Calls can increase in value, and you have a paper loss. But usually this is a temporary event, and the volatility reduces. Theta will often save the day, as the time value of the option rapidly diminishes to zero. In addition, learn to sell Iron Condors when implied volatility is high (such as just before an earnings announcement), and Vega will be on your side.
There are other Greeks such as Rho (which is related to interest rates) but it doesn't affect our trading at this time, so we ignore it.
+++++++++++++++++++++++++++++++++++++++++++++++++
So now here's your review and homework.
1. Complete your answers to the 10 questions below. Have fun and compare you answers with others. If you think you might have missed an answer, go back over the review notes.
2. If you have a copy of "Trading Options for Dummies," read the first three chapters. When you find any unfamiliar terms, check the Glossary at the back and/or contact your class partner.
This is a summary of a class lecture. All rights reserved. Copyright 2014 - 2015 Graeme Sharrock and Honolulu Options Traders, LLC.